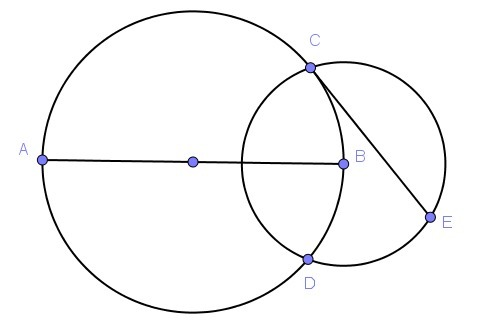
Две окружности пересекаются в точках CC и DD. Точка BB — центр второй окружности, а отрезок ABAB — диаметр первой. Из точки CC провели касательную к первой окружности, которая пересекает вторую окружность в точке EE, отличной от CC. Найдите радиус первой окружности, если радиус второй равен 25, а длина отрезка CECE равна 30.