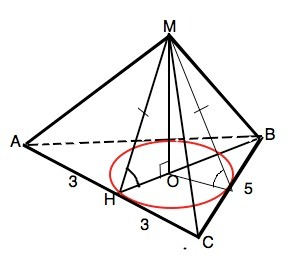
Грани пирамиды наклонены к плоскостью основания под равными углами, следовательно, проекции их высот на основание равны радиусу вписанной в треугольник (основание) окружности. ⇒
высоты боковых граней, как наклонные из одной точки с равными проекциями, равны.
Площадь S полной поверхности пирамиды - сумма площадей основания (S1) и боковой поверхности (S2).
S=S1+S2
В основании пирамиды МАВС - равнобедренный треугольник АВС; АВ=ВС=5 см, АС=6 см.
Высота основания ВН делит треугольник на два равных прямоугольных треугольника.
ВН=√(AB²-AH²)=√(25-9)=4
ОН- радиус вписанной окружности. r=S/p, где р - полупериметр ∆АВС.
S1=BH•AC:2=12 см²
р=(5+5+6):2=8 см
r=12/8=1,5 см
МН=ОН:cos60°=1,5:1/2=3
S2=3•h=3*8=24 см²
S=12+24=36 см²