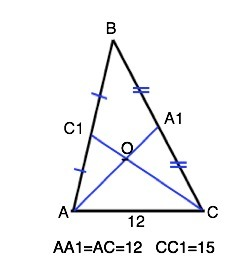
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒
АО=12:3•2=8
CO=15:3•2=10
Весь треугольник разделяется своими тремя медианами на шесть равновеликих (равных по площади) треугольников. Если провести медиану из В к АС, то
площадь ∆ АОС =2•1/6 S ABC=1/3 S ABC
По т.Герона площадь треугольника
S=√(р•(р-а)•(p-b)•(p-c), где а, b и c - стороны треугольника, р - его полупериметр.
р ∆ АВС=(12+8+10):2=15
По т.Герона S ∆AOC=√15•(15-8)•(15-10)•(15-12)
S ∆ AOC=√15•7•5•3=15√7⇒
S ∆ ABC=3•15√7=45√7 (ед. площади)