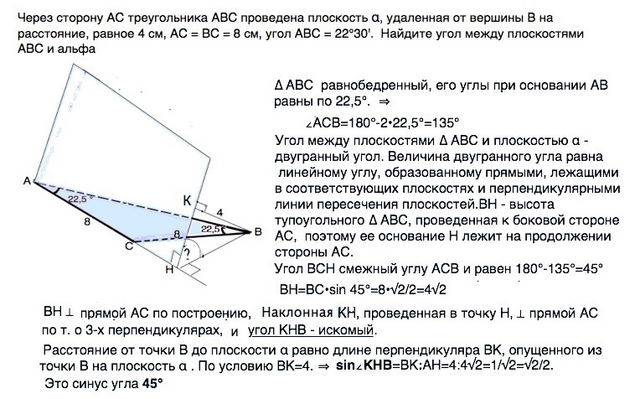
∆ АВС - равнобедренный, его углы при основании АВ равны по 22,5°, поэтому угол АСВ=180°-2•22,5=135°.
Угол между плоскостью ∆ АВС и плоскостью α - двугранный, и его величина равна линейному углу, образованному прямыми, лежащими в соответствующих плоскостях и перпендикулярными линия их пересечения.
ВН - высота тупоугольного ∆ АВС, проведенная к боковой стороне АС, поэтому её основание Н лежит на продолжении стороны АС.
∠ВСН - смежный ∠АСВ и равен 180°-135°=45°
ВН=ВС•sin45°=8•√2/2=4√2
ВН перпендикулярна прямой АС по построению;
наклонная КН, проведенная в точку Н, перпендикулярна прямой АС по теореме о 3-х перпендикулярах, ⇒ ∠КНВ - искомый.
Расстояние от вершины В до плоскости α равно длине перпендикуляра ВК, опущенного из точки В на плоскость α.
По условию ВК=4, ⇒sin∠КНВ=ВК:АН=4:4√2=1/√2=√2/2
Это синус 45°.
Угол между плоскостью АВС и плоскостью α равен45°.