Отрезки касательных из одной точки до точек касания с окружностью равны.
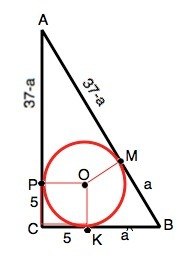
Обозначим точки касания на АС -Р, на АВ-М, на ВС-К.
Пусть КВ=а.
Тогда КВ=МВ=а, АМ=АР=37-а.
Катет АС=37-а+5=42-а.
Катет ВС=а+5.
Гипотенуза АВ=37.
По т.Пифагора
АВ*=АС*+ВС²
Подставив найденные значения катетов и гипотенузы в это уравнение, получим квадратное уравнение
2а²-74а+420.
Решение этого уравнения дает два корня: 30 и 7, оба подходят, т.к. равны отрезкам АВ.
Тогда АС=42-7=35,
ВС=7+5=12
S ∆АВС=АС•BC:2=35•12:2=210 см²