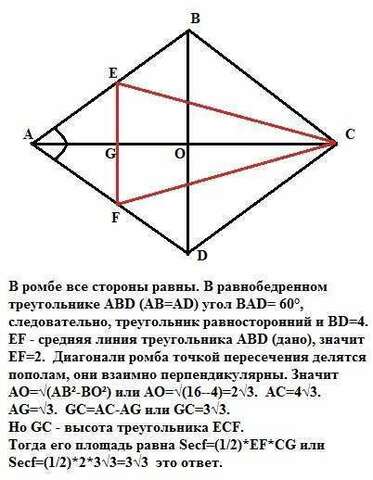
В ромбе все стороны равны. В равнобедренном треугольнике АВD (АВ=АD) угол ВАD= 60° (дано), следовательно, треугольник равносторонний и ВD=4.
EF - средняя линия треугольника АВD (дано), значит EF=2.
Диагонали ромба точкой пересечения делятся пополам, они взаимно перпендикулярны. Значит
АО=√(АВ²-ВО²) или АО=√(16--4)=2√3. АС=4√3.
AG=√3. GC=AC-AG или GC=3√3.
Но GС - высота треугольника ECF.
Тогда его площадь равна Secf=(1/2)*EF*CG или
Secf=(1/2)*2*3√3=3√3 это ответ.