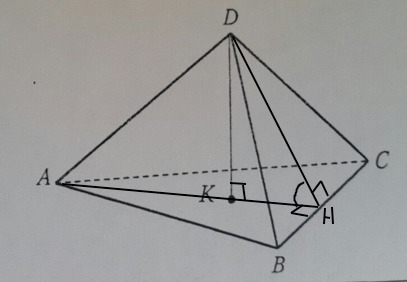
Найдите величину двугранного угла при ребре основания правильной пирамиды DABC со стороной 16√3 и высотой 8.
* * *
Величина двугранного угла равна величине его линейного угла, т.е. угла между лучами, проведенными в его гранях перпендикулярно ребру в одной точке.
Отметим на ВС ее середину точку Н. Высота АН основания =медиане и перпендикулярна ВС.
Высота DH грани - перпендикулярна ВС. Угол DHA - искомый.
К - центр треугольника и центр вписанной окружности в него. КН=1/3 высоты АН.
AH=(16√3)•√3:2=24
KH=24:3=8
В прямоугольном ∆ DКH катеты DK=HK=8, следовательно его острые углы равны 45°
Величина данного двугранного угла равна 45°