Будем считать, что в условии опечатка и дано BC=4√3, а не АС. Иначе, как будет видно из решения, радиус описанной окружности может принимать бесконечно много значений.
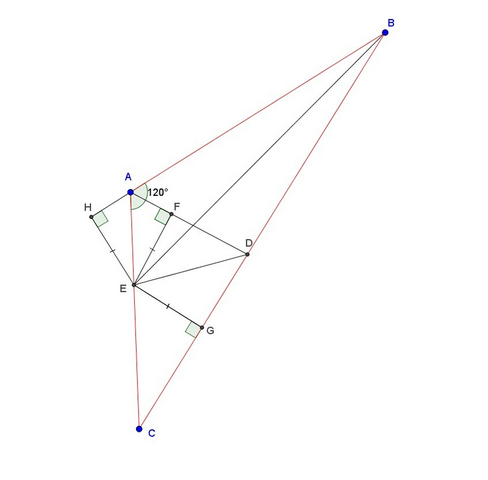
Проведем перпендикуляры EH, EF, EG к прямым BA, DA и BC соответственно (см. рисунок). Т.к. Е лежит на биссектрисе угла ABC, то Е равноудалена от прямых BA и ВС, т.е. EH=EG. Т.к. Е лежит на биссектрисе угла CDA, то E равноудалена от прямых DA и BC, т.е. EF=EG, значит EH=EF, т.е. ∠EAH=∠EAF=∠DAB. С другой стороны, ∠EAH+∠EAF+∠DAB=180°, откуда ∠DAB=60° и, значит, ∠BAC=120°. Тогда, если BC=4√3, то по т. синусов R=BC/(2sin∠BAC)=4√3/(2·√3/2)=4.
Если же все-таки фиксирована АС=4√3, то понятно, что двигая точку B по стороне угла в 120°, будем получать треугольники ABC со сколь угодно большой стороной AB и при этом будет выполняться условие задачи. Т.е. радиус описанной окружности может быть любым числом большим 4.