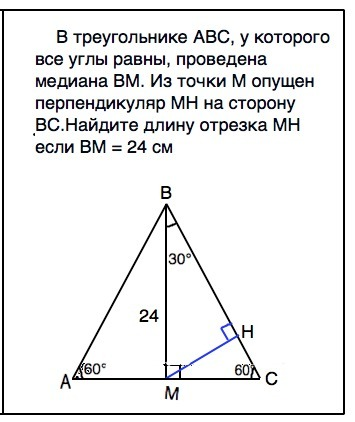
Так как углы ∆ АВС равны, каждый из них равен 60°, а сам треугольник - правильный.
Перпендикуляр ВМ -высота, медианаи биссектриса∆ АВС.
∆ ВМС - прямоугольный. В ∆ ВМН МН перпендикулярен ВС, он противолежит углу МВН, равному 30° ( т.к. ВМ - биссектриса). ⇒
МН равен половине гипотенузы ВМ .
МН=ВМ:2=12 см