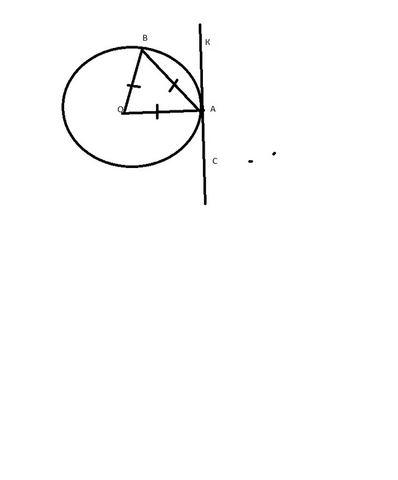Вспомним свойство касательной :
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания(образует 90*).
Проведем из центра окружности О два радиуса в точки А и В , у нас получился равносторонний треугольник ОАВ - все углы по 60*.
Обозначим на касательной для удобства две точки К и С,как показано на рисунке( они расположены в противоположных сторонах от точки А).
∠ОАК =90*
∠ОАВ=60*
∠ВАК=∠ОАК -∠ОАВ
∠ВАК=90*-60*
∠ВАК=30*
Мы нашли угол, образованный хордой АВ, длина которой равна радиусу окружности, и касательной, проходящей через точку А.
Но хорда АВ и касательная КС также образуют ∠ОАС, найдём его.
∠ОАС и ∠ВАК это смежные углы, их сумма 180*
∠ОАС= 180*-∠ВАК
∠ОАС= 180*-30*
∠ОАС= 150*