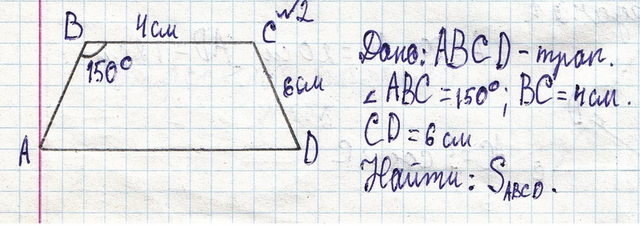
Площадь трапеции равна:
S=(a+b)*h/2 - где а и b - основания трапеции; h- высота
360 - 2*150=60 (град)
60 : 2=30 (град) - углы A и D
Найдём h из sinD=sin30 sin30=1/2
sinD=sinA=h/CD=h/AB
1/2=h/6
h=1/2*6=3 (см)
Найдём нижнее основание:
если мы опустим высоты из углов B и С , то получим два прямоугольных треугольника, из которых мы найдём нижний катет, который является частью нижнего основания. Их здесь два.
По теореме Пифагора найдём нижний катет:
6²-3²=36-9=25 √25=5 (см)
Нижнее основание равно:
4см + 2*5см =4+10=14 (см)
Отсюда:
S=(4+14)*3/2=9*3=27 (см²)
Ответ: S=27см²