Помогите пожалуйста. желательно ** листочке и подробно. Тк надо не тупо списать, а...

Question

Дан 1 ответ

Правильный ответ

Нам придется применять теорему косинусов:

$c^2=a^2+b^2-2ab\cos\gamma,$

где a, b, c - стороны треугольника, а $\gamma$ - угол, лежащий против стороны c.

Из тр-ка ADB

$BD^2=2^2+6^2-2\cdot 2\cdot 6\cdot \cos 60^{\circ}=28; \ BD=2\sqrt{7}.$

Из тр-ка ADC

$CD^2=4^2+6^2-2\cdot 4\cdot 6\cdot \cos 60^{\circ}=28; \ CD=2\sqrt{7}.$

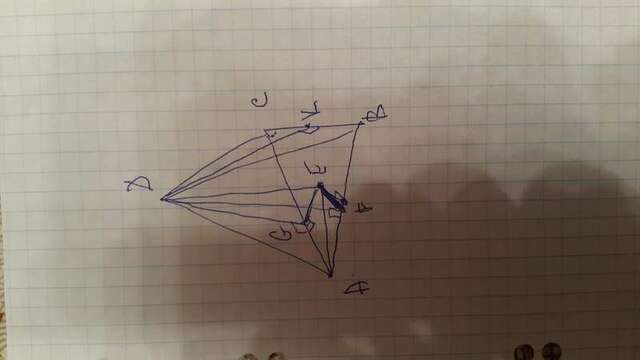
Опустим высоту DE на основание ABC. Из точки E опустим перпендикуляры EF и EG на стороны AB и AC соответственно. По теореме о трех перпендикулярах DF перпендикулярно AB, DG перпендикулярно AC. Прямоугольные треугольники ADF и ADG равны по общей гипотенузе и острому углу. Поэтому DF=DG, а тогда равны треугольники DFE и DGE, откуда EF=EG, то есть точка E лежит на биссектрисе угла A. Значит, углы FAE и GAE равны 45 градусам.

AF=AG мы ищем как катеты, лежащие против угла в 30 градусов - такой катет равен половине гипотенузы; AF=AG=6/2=3. Вторые катеты ищем или из теоремы Пифагора, или с помощью тригонометрии. Так или иначе, $DF=DG=3\sqrt{3}$ . Далее из равнобедренного прямоугольного треугольника AEF (или равного ему треугольника AEG) находим EF=AF=3, а из треугольника DFE (или из равного ему DGE) по теореме Пифагора находим DE - высоту пирамиды:

$DE^2=DF^2-FE^2=27-9=18; DE=3 \sqrt{2.}$

Площадь основания ABC равна половине произведения катетов:
$S_{ABC}=\frac{1}{2}2\cdot 4=4.$

Объем пирамиды равен $V=\frac{1}{3}S_{ABC}\cdot DE=4\sqrt{2}.$

Далее найдем площадь треугольника BDC, запишем объем пирамиды через площадь этой грани и высоту, на нее опущенную, приравняем к полученному выше объему, откуда найдем неизвестную высоту. Требуемое расстояние, очевидно, в 2 раза меньше этой высоты.

$BD=BC=2\sqrt{7}$ мы уже получили ранее, BC находим из прямоугольного треугольника ABC:

$BC^2=AB^2+AC^2=4+16=20; \ BC=2\sqrt{5}.$

Для того, чтобы найти площадь треугольника BDC, опустим высоту DK на BC (в силу равнобедренности этого треугольника высота будет одновременно медианой и биссектрисой);

$DK^2=DB^2-BK^2=28-5=23; DK=\sqrt{23}.$

$S_{BDC}=\frac{1}{2}BC\cdot DK=\sqrt{115}.$

Приравняв друг к другу две формулы для вычисления объема пирамиды и сократив одну треть, получаем, что для нахождения неизвестной высоты, нужно произведение известной высоты и площади грани разделить на площадь второй грани. Поэтому высота, опущенная на грань BCD, равна

$H=\frac{DE\cdot S_{ABC}}{S_{BDC}}=\frac{3\sqrt{2}\cdot 4}{\sqrt{115}}= \frac{12\sqrt{230}}{115}$

То, что требуемое расстояние в 2 раза меньше, предлагается доказать самостоятельно. Впрочем, интуитивно это совершенно очевидно: представьте себе лестницу, приставленную к стене под некоторым углом. Если расстояние от верхней ступеньки до пола известно, то, спустившись по лестнице до ее середины, уменьшим расстояние до пола в два раза.

Ответ: $\frac{6\sqrt{230}}{115}$

Замечание. Ответ получился не самый приятный. Но искать ошибку, когда ночь на дворе, не слишком приятно. Поэтому извините, если что не так.

yugolovin_zn (64.0k баллов) 13 Май, 18