Площадь окружности:
Sо = пR², отсюда: R = √(So/п) = 4 (см).
Если в трапецию вписана окружность, то её диаметр — средняя линия трапеции (назовём её MN). Тогда средняя линия — два радиуса окружности:
MN = 2R.
Формула средней линии:
MN = 2R = (BC + AD)/2, отсюда: BC + AD = 4R.
BC + AD = 4*4 = 16 (см).
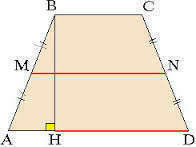
Проведём высоту трапеции из вершины В к основанию AD, точку пересечения высоты и AD назовём Н.
Если в трапецию можно вписать окружность, то сумма её противолежащих сторон равна:
AB + CD = BC + AD.
Не забываем, что наша трапеция равнобедренная (AB = CD).
2AB = BC + AD,
2AB = 16,
AB = 8 (см).
Угол BAD = 180° - 150° = 30°.
Рассмотрим треугольник ABH — прямоугольный. Против угла в 30° лежит катет, равный половине гипотенузы:
AB = 2BH, отсюда: BH = AB/2 = 8/2 = 4 (см).
Площадь трапеции:
S = (BC + AD)/2 * BH,
S = 16/2 * 4 = 32 см².
Ответ: 32 см².