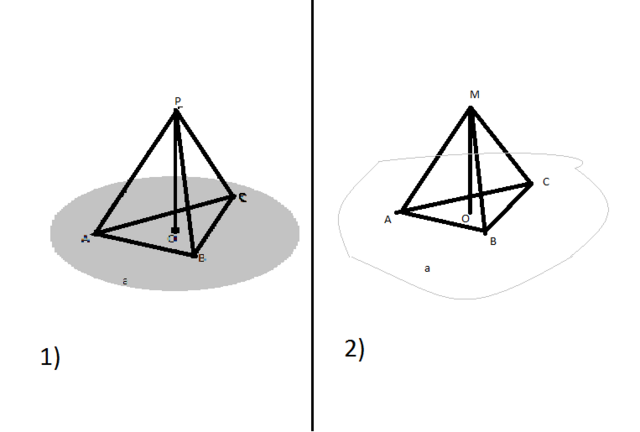
1) Точка Р равноудалена от всех вершин треугольника, стороны которого равны 6 см, 6 см и...

Question

1) Точка Р равноудалена от всех вершин треугольника, стороны которого равны 6 см, 6 см и 8 см. Расстояние от точки Р до плоскости треугольника равна 2 корень 14 см. вычислите расстояние от точки Р до вершин треугольника.

2) Угол А остроугольного треугольника АВС равен 45 градусов, ВС=12 см. Точка М удалена от его плоскости на 6 см и находится на одинаковом расстоянии от всех вершин треугольника. Вычислите расстояние МА, МВ и МС.

---

Answer 1

1.
РО⊥АВС.
ΔРОА = ΔРОВ = ΔРОС по катету и гипотенузе (РО - общий катет, РА = РВ = РС по условию), значит
ОА = ОВ = ОС  = R - радиус окружности, описанной около ΔАВС.
По формуле Герона:
Sabc = √(p(p - AB)(p - AC)(p - BC)) = √(10 · 4 · 4 · 2) = 8√5 см²
Sabc = AB·AC·BC / (4R)
8√5 = 6·6·8 / (4R) = 72 / R
R = 72 / (8√5) = 9 / √5 = 9√5/5 см
ΔРОА: ∠РОА = 90°, по теореме Пифагора
           РА = √(РО² + АО²) = √(56 + 81/5) = √(361/5) = 19 / √5  = 19√5/5 см

2.
МО⊥АВС.
ΔМОА = ΔМОВ = ΔМОС по катету и гипотенузе (МО - общий катет, МА = МВ = МС по условию), значит
ОА = ОВ = ОС  = R - радиус окружности, описанной около ΔАВС.
R = BC / (2sin∠A) = 12 / (2 · √2/2) = 12 / √2 = 6√2 см
Из прямоугольного ΔМОА по теореме Пифагора:
МА = √(МО² + АО²) = √(36 + 72) = √108 = 6√3 см