Область допустимых значений ОДЗ:
6+5х-х²≥0, сначала найдем решение для
6+5х-х²=0
х²-5х-6=0
D=25+24=49
х₁ = (5-7)/2 = -1
х₂=(5+7)/2 = 6
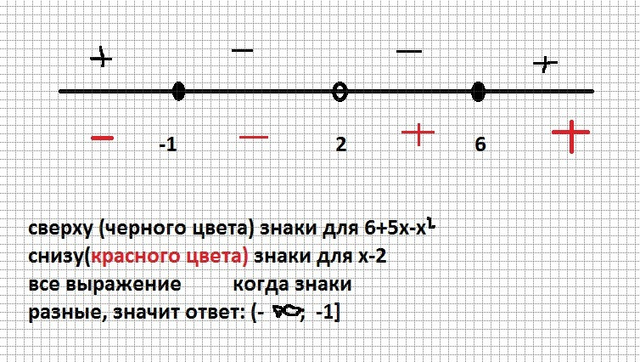
х≤ -1 и х≥6,
а также х-2≠ 0, х≠ 2
тогда ОДЗ: х∈(-∞;-1)∪(6;+∞)
решаем методом интервалов: решением будет область, где встречаются разные знаки у числителя и знаменателя
Ответ: (-∞; -1] (квадратная скобка после -1)