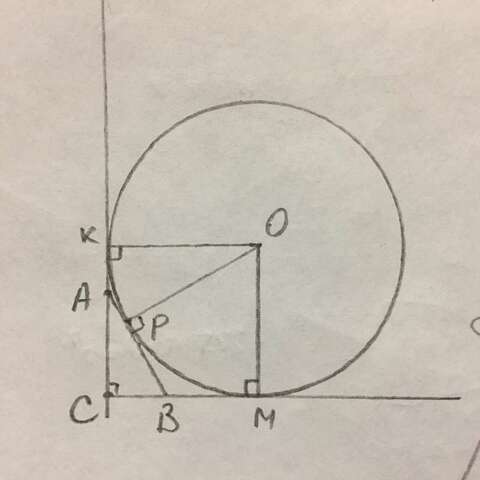R=3, R=ОК=ОМ=18.
СК=СМ=R=18.
АК=АР и ВР=ВМ как касательные к окружности, проведённые из одной точки.
Р(АВС)=АР+ВР+АВ+АС=АК+ВМ+АС+ВС=СК+СМ=2R=2·18=36.
P=a+b+с ⇒ a+b=P-c=36-c,
r=(a+b-c)/2 ⇒a+b=2r-c=6+c.
36-c=6+c,
2c=30,
c=15.
a+b=36-c=36-15=21 ⇒ b=21-a.
По теореме Пифагора a²+b²=c²,
a²+(21-a)²=15²,
а²+441-42а+а²=225,
2а²-42а+216=0, решаем квадратное уравнение, получаем:
а1=9, а2=12,
b1=21-9=12, b2=21-12=9.
Ответ: больший катет равен 12.