Для начала попробуем разобрать один из способов решения подобных задач.
Рассмотрим контрольный пример.
Входные данные:
5 - это количество врачей, т.е. нижеследующих строчек.
2 3 5 - 1-й врач. У него 2 предшественника - врачи 3 и 5
2 3 5 - 2-й врач. У него 2 предшественника - врачи 3 и 5
1 5 - 3-й врач. У него 1 предшественник - врач 5
3 1 3 5 - 4-й врач. У него 3 предшественника - врачи 1, 3 и 5
0 - 5-й врач. У него нет предшественников.
Вариант результата: 5 3 1 2 4 - в таком порядке посещаются врачи.
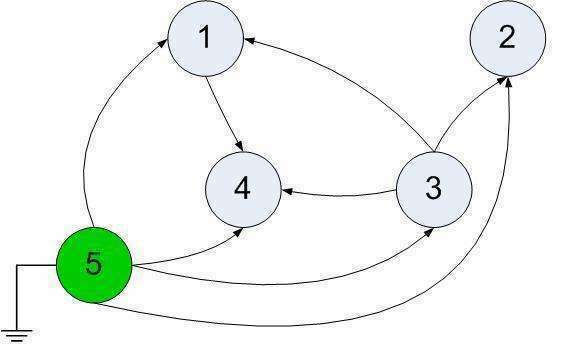
Изобразим эти данные графически. В кружочках проставим номера врачей и соединим кружочки стрелками, отображающими взаимосвязи (первое вложение). Полученный рисунок - ни что иное, как ориентированный граф.
Решение будет состоять в поиске порядка посещения всех вершин графа ("врачей") в соответствии с доступными путями ("очередностью").
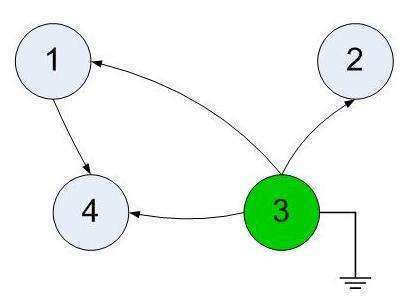
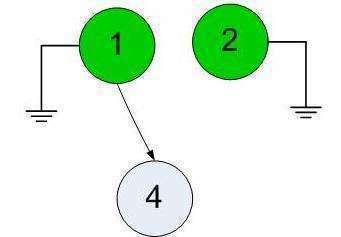
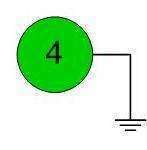
Очевидно, что первой нужно посетить вершину, из которой пути только выходят. Если ни одной такой вершины нет - задача решения не имеет. В нашем случае такая вершина есть - номер 5 и она помечена зеленым. После посещения мы удаляем эту вершину и все ведущие из нее пути. Получаем картину, представленную вторым вложением. Повторяем наше рассуждение и находим вершину 3. Снова удаляем её и выходящие из нее пути. В третьем вложении мы видим, что доступны сразу две вершины - 1 и 2. Их можно посетить в любом порядке, т.е. решение не единственное. Будем придерживаться порядка возрастания и и вычеркнем 1 с путём, а затем и 2. В чевертом вложении остается свободная вершина 4. Посещаем её, вычеркиваем - граф исчез, задача решена. И порядок посещения совпал с контрольным решением.
Теперь, когда "ручное" решение понятно, можно строить алгоритм.
Мы использовали граф, а граф в программировании представляется парой множеств: множеством вершин и множеством путей, их соединяющих.
Эти множества классически представляются двумя матрицами - матрицей смежности (отображает вершины и наличие связей) и матрицей инцидентности (отображает направление связей и, возможно, длины путей). Другие варианты - списки или деревья, но они требуют набора процедур для соответствующих манипуляций.
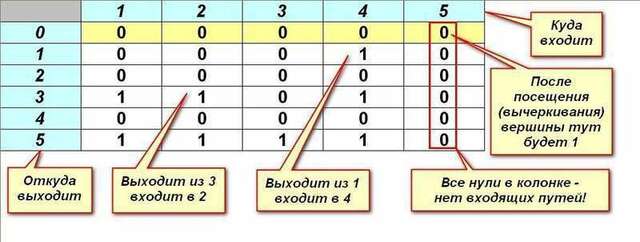
В связи с относительной простотой задачи был выбран собственный вариант отображения графа на квадратную матрицу размера (n+1)×n, где n- количество вершин (врачей). Первая строка матрицы является служебной, остальные отображают граф. В пятом вложении приведена принятая схема отображения. Собственно, из этой схемы понятна основная идея реализации. Создаем матрицу, расписываем её нулями, затем заносим единицы, создавая связи. Решение состоит в последовательном переборе колонок до нахождения столбцов, содержащих все нули. Найденный столбец "вычеркивается" (записывается 1 в нулевой строке), а его номер - это номер посещенной вершины. Процесс повторяется, пока в служебной строке не будут все единицы, либо пока не будет n раз сделан проход по столбцам (от зацикливания при отсутствии решения).
Поскольку программа может показаться нетривиальной, в нее внесены операторы отладки, позволяющие по шагам проследить решение. Как управлять отладкой, ясно из комментариев. Если отладка не нужна, достаточно из программы удалить все строки, отмеченные \\-
// PascalABC.NET 3.2, сборка 1417 от 28.03.2017
// Внимание! Если программа не работает, обновите версию!
begin
var n:=ReadInteger; // первая строка - число врачей
var a:=MatrFill(n+1,n,0); // матрица посещений
var t:integer;
for var i:=1 to n do begin // цикл ввода по каждому врачу
var k:=ReadInteger; // количество врачей-предшественников
for var j:=1 to k do begin
Read(t);
a[t,i-1]:=1
end;
end;
t:=0;
var res:='';
var debug:=true; //- debug:=false блокирует отладочную выдачу
if debug then begin //-
Writeln('исходная матрица'); //-
a.Println(2); Writeln //-
end; //-
for var m:=1 to n do begin
for var j:=1 to n do begin
var c:=a.Col(j-1);
if c[0]=0 then begin
if c.All(x->x=0) then begin
Res+=j+' ';
if debug then Writeln(Res); //-
a[0,j-1]:=1;
for var i:=0 to n-1 do a[j,i]:=0;
if debug then begin //-
a.Println(2); Writeln //-
end //-
end
end;
end;
if a.Row(0).All(x->x=1) then begin t:=1; break end;
end;
if t=0 then Writeln(-1)
else Writeln(Res)
end.
Пример решения с выключенной отладкой
5
2 3 5
2 3 5
1 5
3 1 3 5
0
5 3 1 2 4
Пример со включенной отладкой (можно исходные данные для удобства все писать в одной строке)
5 2 3 5 2 3 5 1 5 3 1 3 5 0
исходная матрица
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 1 0 1 0
0 0 0 0 0
1 1 1 1 0
5
0 0 0 0 1
0 0 0 1 0
0 0 0 0 0
1 1 0 1 0
0 0 0 0 0
0 0 0 0 0
5 3
0 0 1 0 1
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
5 3 1
1 0 1 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
5 3 1 2
1 1 1 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
5 3 1 2 4
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
5 3 1 2 4