|x| = -x при x<0 <br>|x| =x при х≥0
|2x-1|=-(2x-1) при 2x-1<0, 2x<1, x<1/2<br>|2x-1|=2x-1 при x≥1/2
|x-3|=-(x-3) при x-3<0, x<3</span>
|x-3|=x-3 при x≥3
Поэтому разобъем ось х на интервалы
1. x<0<br>F(x) = -x - (2x-1) - (x-3)=-x-2x+1-x+3=-4x+4
2. 0≤x<1/2<br>F(x) = x - (2x-1) - (x-3)=x-2x+1-x+3=-2x+4
3. 1/2≤x<3<br>F(x) = x + (2x-1) - (x-3)=x+2x-1-x+3=2x+2
4. x≥3
F(x) = x + (2x-1) + (x-3)=x+2x-1+x-3=4x-4
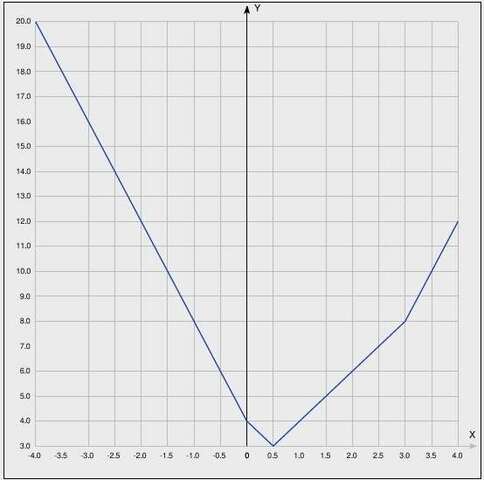
на каждом из четырех интерывалов строим свою функуцию, см. вложение