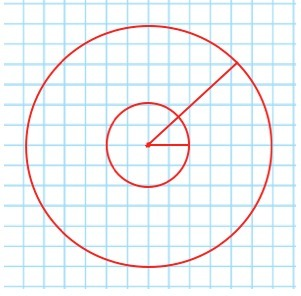
Площадь кругового кольца равна разности между площадями большего и меньшего кругов, ограниченных окружностями с общим центром.
Пусть радиус меньшего круга r. Тогда большего – 3r.
S1=πr² S2=π•(3r)² =9πr²
S=π(3r)²-πr²=8πr²
По условию 8πr²=8 ⇒ πr²=1см²
S1=1 см² – площадь меньшего круга
S2=9 см² – площадь большего круга.
Их площади меньшего круга найдем его радиус.
πr²=1⇒ r²=1/π ⇒ r=√(1/π )или, если домножить знаменатель и числитель дроби под корнем на π, получим r=(√π):π
3r=3•√(1/π )
-------------
Формула площади кругового кольца S=π(R²-r²)