На диаграммах изображены:
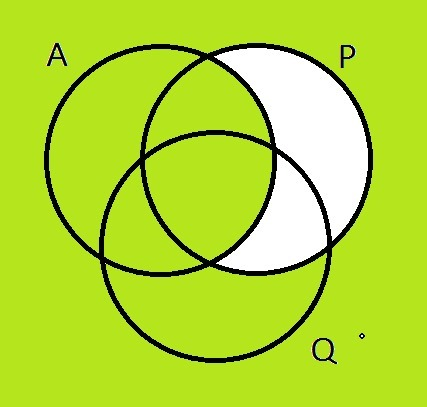
- зеленым цветом - множество, для которого верно утверждение (x ∈ P) → (x ∈ A) (оно состоит из элементов, не входящих в P или входящих в A)
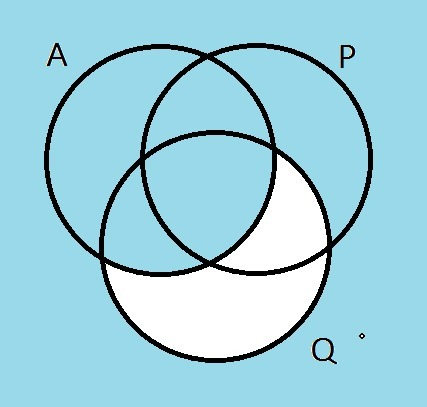
- голубым цветом - множество, для которого верно утверждение ¬(x ∈ A) → ¬(x ∈ Q) (оно состоит из элементов, входящих в A или не входящих в Q)
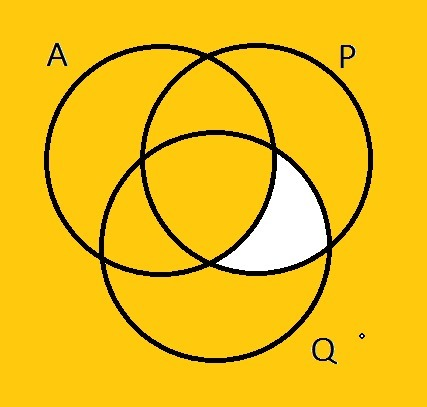
- золотистым цветом - множество, для которого верно утверждение из условия, оно включает области, которые были закрашены хотя бы 1 раз.
Получается, что какое бы ни было A, утверждение будет неверным для x из множества элементов, лежащих в P и Q, но не лежащих в A. Так как по условию утверждение верно для всех x, то незакрашенное множество должно быть пусто, и A содержит все элементы P ∩ Q = {3, 9, 15, 21}.
Наименьшая сумма будет, если в A больше никаких элементов нет. Тогда ответ
3 + 9 + 15 + 21 = 48