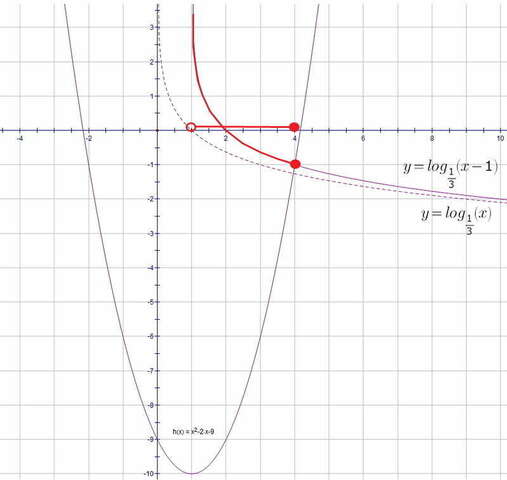
Решение графическое...
1) ОДЗ для логарифма: x > 12) квадратный трехчлен x²-2x-9 = (х-1)² -10 это парабола, ветви вверх
D=4+36=40 имеет корни: х₁ = 1-√10 (<0) x₂ = 1+√10 (≈4.1)и вершину в точке (1; -10)<br>знак неравенства "≥", следовательно, нужно ответить на вопрос:
для каких (х) график логарифмической функции "выше" параболы))
логарифм по основанию 1/3 - функция убывающая, пересекает ось ОХ при х=2, в этой точке парабола (1²-10=-9) расположена ниже и уже возрастает, т.е. график логарифма будет выше параболы ДО точки пересечения с нею))) осталось найти эту точку... по графику это не трудно сделать...
решение: х ∈ (1; 4]
log₁/₃(4-1) = log₁/₃(3) = -1
4²-2*2-9 = 16-8-9 = 16-17 = -1