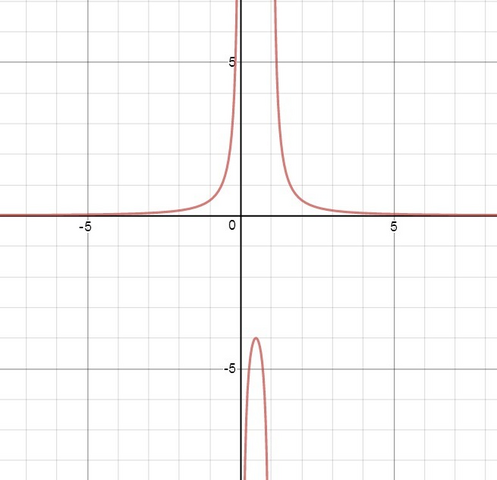
1) Область определения: х≠0; х≠1
y`=-1/(x*(x-1))^2 * (x*(x-1))`=-(2x-1)/(x^2-x)^2
y`=0
2x-1=0
x=1/2- точка максимума, так как при переходе через точку производная меняет знак с + на -
y`(-10) =-(-21)/(...)^2>0
y`(10)=-(19)/(...)^2 <0<br>
y(1/2)=1/(1/2)*(1/2-1)=-4
x=0 и х= 1 вертикальные асимптоты.
limₓ →₋₀1/x*(x-1)=+∞
limₓ →₊₀1/x*(x-1)=-∞
limₓ →₁₋₀1/x*(x-1)=-∞
limₓ →₁₊₀1/x*(x-1)=+∞
imₓ →∞1/x*(x-1)=0
y=0 - горизонтальная асимптота
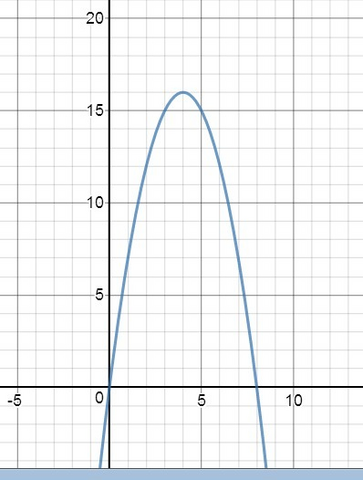
2) ОДЗ:(-∞;+∞)
y`=8-2x
y`=0
8-2x=0
x=4
_+__ (4) _ -__
x=4 - точка максимума, производная меняет знак с + на -.
у(4)=8*4-4^2=32-16=16
Точки пересечения с осями координат
8х-х²=0
х(8-х)=0
х=0 8-х=0⇒х=8
(0;0) и (8;0)