Дан прямоугольный параллелепипед ABCD A1 B1C1 D1 и длина рёбер с общей точкой: AB=5 ед....

Question

Дан прямоугольный параллелепипед ABCD A1 B1C1 D1 и длина рёбер с общей точкой:
AB=5 ед. изм.
AD=20 ед. изм.
AA1=4 ед. изм.
Определи длину диагонали, имеющей общую точку с данными ребрами.

Comments

d² =a² +b²+c² =√(5²+20² +4²) = √(25+400 +16) = √441 =21

Answer 1

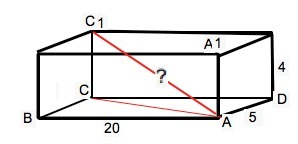
В прямоугольном параллелепипеде все грани  параллелепипеда – прямоугольники. Диагональю параллелепипеда называется отрезок, который соединяет его противоположные вершины. 

Все ребра данного параллелепипеда, выходящие из одной вершины,  известны. 

Проведем диагональ АС1. 

АС1=√(AC²+CC1²)

CC1=AA1=4

AC²=(AB²+BC²)=425

BC=AD=5

AC1²=(425+16)=441

AC1=√441=21 ед. длины

Мы вывели таким образом известную формулу длины диагонали прямоугольного параллелепипеда:  

•Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. 

d²=a²+b²+c²

---