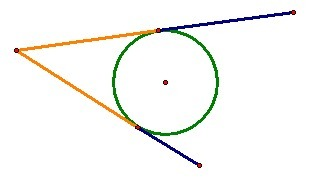
Отрезки касательных проведенные из одной точки касания равны
АТ = АР
радиусы одной и той же окружности равны
ОТ = ОР
радиус окружности перпендикулярен касательной
(если он проведен в точку касания) уг.Р=90 уг.Т=90
мы имеем 4х угольник у которогого 3 прямых угла
( а сумма углов четырехугольника = 360 ) уг.О=90
мы доказали что АТОР - прямоугольник у которого
АТ = АР и ОТ = ОР
поскольку у прям-ка противоположные стороны равны
то АР = ОТ
тогда у АТОР все стороны равны
по определению правильный многоугольник тот
у которого все углы равны и все стороны равны
ЧТД