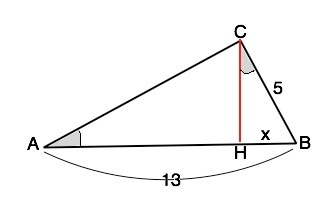
Пусть дан ∆ АВС, ∠С=90°. АВ=13; ВС=5.
Решить эту задачу можно разными способами.
Способ 1.
Прямоугольный треугольник с катетом 5 и гипотенузой 13 относится к Пифагоровым тройкам с отношением сторон 5:12:13. ⇒ АС=12 ( можно найти и по т.Пифагора)
sin∠CAB=ВС/АВ=5/13
В прямоугольном ∆ СНА ∠CAH=∠CAB ⇒ CH/AC=5/13
CH=5•12:13
CH=60/13
* * *
Способ 2
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.
СВ²=АВ•BH
25=13•BH⇒
BH=25/13
CH=√(BC²-BH²)=√(25•144:169)=60/13=4⁸/₁₃
* * *
При желании можно найти СН и другими способами.