1) 4x^2 - 24x - y^2 - 2y + 31 = 0
4(x^2 - 6x) - (y^2 + 2y) + 31 = 0
Выражения в скобках дополним до полных квадратов.
4(x^2 - 6x + 9) - 4*9 - (y^2 + 2y + 1) + 1 + 31 = 0
4(x - 3)^2 - (y + 1)^2 - 36 + 1 + 31 = 0
4(x - 3)^2 - (y + 1)^2 - 4 = 0
4(x - 3)^2 - (y + 1)^2 = 4
(x - 3)^2 - (y + 1)^2/4 = 1
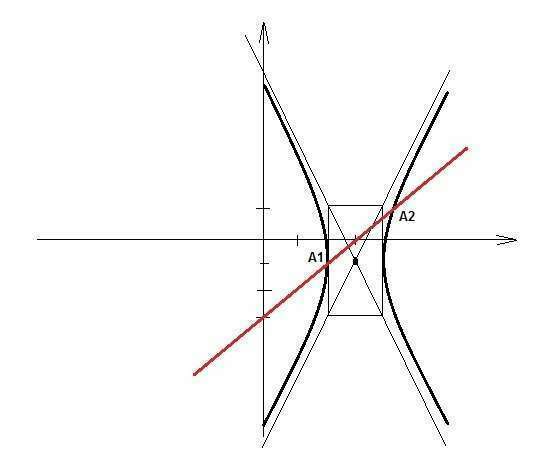
Это гипербола с центром A(3; -1) и полуосями a = 1; b = 2
2) x - y - 3 = 0
y = x - 3
Это прямая.
Они пересекаются в двух точках. Можно это показать графически.
А можно подставить y из 2 ур-ния в 1 ур-ние и решить его.
4y^2 - (y + 1)^2 = 4
4y^2 - y^2 - 2y - 1 - 4 = 0
3y^2 - 2y - 5 = 0
(y + 1)(3y - 5) = 0
y1 = -1; x1 = -1 + 3 = 2
y2 = 5/3; x2 = 5/3 + 3 = 14/3
Ответ: А1(2; -1); А2(14/3; 5/3)