AC=AB=17 см, BC=16 см. O - центр описанной окружности. OK перпендикулярно треугольнику...

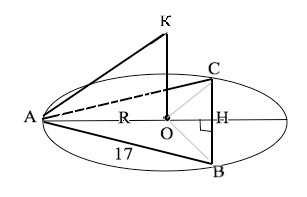
Центр описанной около треугольника окружности находится в точке пересечения срединных перпендикуляров.

Значит, для этого треугольника центр описанной окружности лежит на его высоте АН, т.к. высота равнобедренного треугольника ещё и медиана, поэтому она - срединный перпендикуляр к основанию ВС. .

По т.Пифагора

АН=√(AB²-BH²)=V(289-64)=15 см

$sin(ABC)= \frac{AH}{AB} = \frac{15}{17}$

Примем радиус описанной окружности равным R

По т.синусов $R= \frac{AB}{2*sin(ADC)} = \frac{17*17}{2*15} = \frac{289}{30}$

ОК перпендикулярен плоскости ΔАВС. ⇒ ∆ АОК прямоугольный.

По т.Пифагора

АК=√(AO²+KO²)=√[(83521+22500):2]= ≈10,854 см