На данном отрезке-гипотенузе нужно отметить середину. чтобы найти длину катета, равного её половине. Сделать это можно стандартным способом деления отрезка пополам ( см. ниже возведение перпендикуляра к данной точке - принцип нахождения середины отрезка тот же),
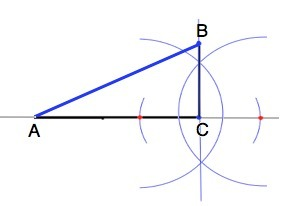
На произвольной прямой отметим вершину будущего прямого угла - т.С.
Отметим с помощью циркуля по обе стороны от нее на равном расстоянии точки 1 и 2 и циркулем с большим раствором из точек 1 и 2 как из центров проведем полуокружности одинакового радиуса до их пересечения по обе стороны от прямой. Прямая, соединяющая точки пересечения, перпендикулярна к первой прямой. Отложим на перпендикуляре отрезок СВ, равный данному катету.
Из т.В раствором циркуля, равным данной гипотенузе, на прямой отметим точку А- третью вершину нужного треугольника.
По построению катет ВС равен половине гипотенузы АВ, равной данному отрезку.
. Синус угла ВАС равен ВС/АВ=1/2. Это синус 30°.
Угол ВСА=90° по построению.
Сумма острых углов прямоугольного треугольника 90°.
Угол АВС=90°-30°=60°