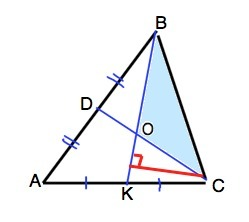
Площадь треугольника можно найти по формуле S=a•h:2 , где а- основание, h- высота, проведенная к нему.
Если у треугольников равны основания и высоты, то их площади равны.
В треугольниках АВК и СВК основания АК=КС, высота из В – общая. Площади этих треугольников равны половине 0,5•SABC.
Следовательно, S ∆ ВСК=0,5 S ∆ АВС.
Рассмотрим ∆ КВС. Точка О делит ВК отношении ВО:ОК=2:1.
Это свойство точки пересечения медианы в задачах встречается нередко.
Высота для ∆ ВОС и КОС общая, поэтому площадь ∆ ВОС равна 2/3 площади ∆ КВС.
А т.к. S ∆ КВС=0,5 S ABC, то S ∆ ВОС=1/3 площади ∆ АВС.⇒
S ∆ АВС=3•S ∆ BOC=18 см²