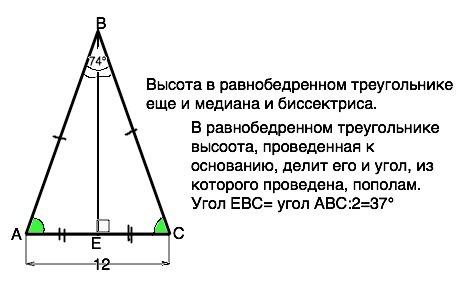
В равнобедренном треугольнике боковые стороны и углы при основании равны, Треугольники АВЕ и СВЕ равны по равным гипотенузе АВ=СВ, общей стороне ВЕ и равным углам А=С.
⇒ АВЕ=∠СВЕ, и поэтому ВЕ - биссектриса угла ВЕ и делит ∠АВС пополам.
∠ЕВС=74°:2=37°.
В приложении дано несколько иное решение. а для чего дана в условии длина АС, - непонятно. Может быть, нужно доказать, что ВЕ не только высота и биссектриса, но и медиана. Из равенства ∆АВЕ=∆СВЕ следует АЕ=СЕ=12:2=6, и отсюда ВЕ - медиана.