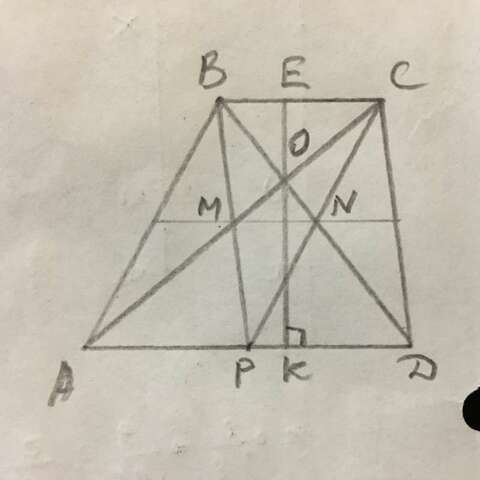АД=2ВС, S(АВСД)=90, ЕК - высота, ЕК=Н.
S(ОМРN)=?
В трапеции треугольники АОД и ВОС подобны (свойство трапеции), значит ЕО:ОК=ВС:АД=1:2 ⇒ ОК:ЕК=2:3. ОК=2Н/3.
Пусть ВС=х, тогда АД=2х.
Площадь трапеции АВСД: S(АВСД)=Н(х+2х)/2=3Нх/2.
S(АОД)=АД·ОК/2=2х·2Н/6=2Нх/3.
АВСР и РВСД - параллелограммы так как ВС=АР=РД и ВС║АД.
Диагонали параллелограммов пересекаются в точках М и N, которые находятся в центрах параллелограммов, значит точки М и N лежат на средней линии трапеции, следовательно высоты треугольников АМР и PND, опущенные на прямую АД, равны Н/2.
Площади треугольников АМР и PND равны т.к. их основания и высоты равны.
S(АМР)=х·Н/4.
Теперь, S(OMPN)=S(AOД)-2S(АМР)=2Нх/3-Нх/2=(4Нх-3Нх)/6=Нх/6.
Найдём отношение известных площадей:
S(АВСД):S(ОМРN)=(3Нх/2):(Нх/6)=9:1
Итак, S(ОМРN)=S(АВСД)/9=90/9=10 - это ответ.