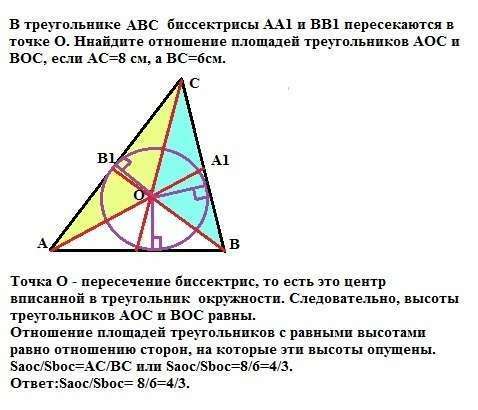
Точка О - пересечение биссектрис, то есть это центр вписанной в треугольник окружности, равноудаленный от сторон треугольника. Следовательно, высоты треугольников АОС и ВОС равны.
Отношение площадей треугольников с равными высотами равно отношению сторон, на которые эти высоты опущены. Saoc/Sboc=АС/ВС или Saoc/Sboc=8/6=4/3.
Ответ:Saoc/Sboc= 8/6=4/3.