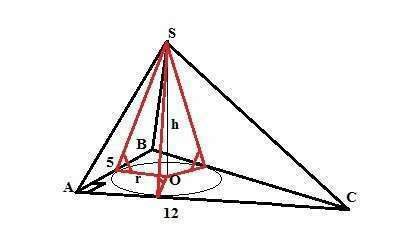
Если боковые грани пирамиды наклонены к плоскости основания под равными углами, то вершина этой пирамиды проецируется в центр вписанной в основание окружности.
Гипотенуза треугольника АВС по Пифагору равна ВС=√(АВ²+АС²)=√(5²+12²)=13.
Площадь основания равна So=(1/2)*AB*AC или
So=(1/2)*5*12=30.
Радиус вписанной окружности равен r=S/p, где S - площадь треугольника, р - его полупериметр.
r=30/15=2.
Тогда высота пирамиды равна SO=r*tg60° или
SO=2*√3 ед.
Высота граней пирамиды - гипотенуза, равна 2r=4, так как в прямоугольном треугольнике, образованном высото1 пирамиды, радиусом вписанной окружности (катеты) и высотой грани (гипотенуза) катет "r"лежит против угла 30°.Тогда площади боковых граней равны:
S1=(1/2)*12*4=24,
S2=(1/2)*5*4=10,
S3=(1/2)*13*4=26, а площадь боковой поверхности равна
S=S1+S2+S3 или S=24+10+26=60 ед².
Ответ: высота пирамиды 2√3 ед., S=60 ед².