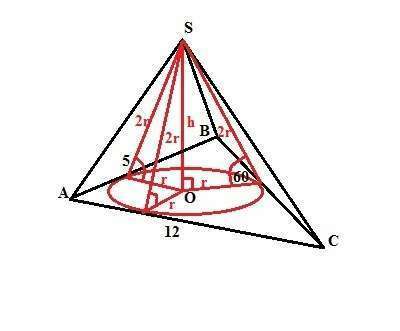
Боковые грани пирамиды наклонены к плоскости основания под одинаковым углам. Следовательно, вершина пирамиды проецируется в центр вписанной в основание окружности.
Радиус вписанной в треугольник окружности равен: r=S/p, где S - площадь треугольника, р - полупериметр треугольника.
Гипотенуза основания по Пифагору равна √(12²+5²)=√169=13.
Тогда р=5*12*13=30 и r=30/30=1.
Найденный радиус - это катет, лежащий против угла 30° в треугольниках, образованных высотой (второй катет) и высотой боковой грани (гипотенуза). Значит высота боковой грани равна 2*r или 2.
Тогда высоту пирамиды найдем по Пифагору: h=√(4-1)=√3.
Площадь полной поверхности пирамиды равна сумме площадей основания и боковых граней (треугольников:
S=(1/2)*5*12+(1/2)*5*2+(1/2)*12*2+(1/2)*13*2=30+5+12+13=60 ед²
Ответ: высота пирамиды равна √3, площадь полной поверхности 60 ед².