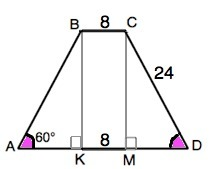
Высоты ВК и СМ из вершин тупых углов трапеции делят ее на прямоугольник ВСМК и два равных прямоугольных ∆ АВК=∆C DM (по гипотенузе и острому углу при А и D).
Углы при В и С в этих треугольниках равны 90°-60°=30°.
АК=DM=24:2=12 ( по свойству катета, противолежащего углу 30°.
КМ=ВС=8 ( т.к. ВСМК - прямоугольник) ⇒
АD=AK+KM+MD=32 (ед. длины)