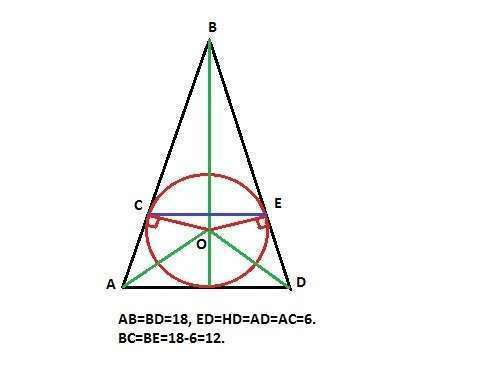
Пусть дан равнобедренный треугольник АВD. Центр вписанной окружности находится в точке О пересечения биссектрис.Значит АО и DО - биссектрисы. Проведем биссектрису ВН. Треугольник равнобедренный, значит ВН является и высотой и медианой. Тогда АН=DН=12:2=6.
Касательные из одной точки к окружности равны (свойство). Следовательно, ЕD=DН=CA=AH=6. ВЕ=ВС=18-6=12 и треугольник СВЕ так же равнобедренный.
Треугольники СВЕ и АВD подобны, так как сли две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны (ВС/ВА=ВЕ/ВD и Коэффициент их подобия равен отношению соответственных сторон, то есть СЕ/АD=12/18=2/3.
Тогда СЕ=АD*(2/3) или СЕ=12*2/3=8.
Ответ: СЕ=8.