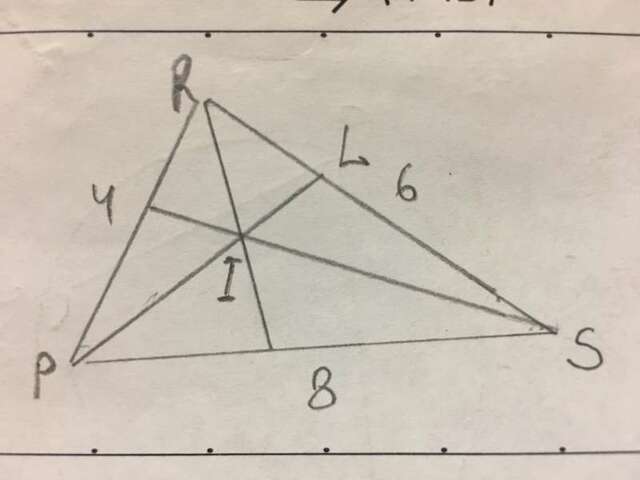
В треугольнике PRL RI - биссектриса, значит по теореме биссектрис:
PR/RL=PI/IL.
Аналогично в тр-ке PSL SI - биссектриса и PS/SL=PI/IL.
Пришли к классической теореме биссектрис для тр-ка PRS:
PI/IL=PR/RL=PS/SL.
Пусть коэффициент подобия дробей PR/RL и PS/SL равен k, тогда:
PS/SL=(PR·k)/(RL·k).
Сложим числители и знаменатели этих подобных дробей:
(PR+PS)/(RL+SL)=(PR+PR·k)/(RL+RL·k)=(PR·(1+k))/(RL·(1+k))=PR/RL.
Но RL+SL=RS, значит:
PI/IL=PR/RL=(PR+PS)/RS=(4+6)/8=10/8=5:4 - это ответ
PS. Таким образом это стандартное отношение отрезков биссектрисы на которые её делит точка пересечения биссектрис треугольника.
В общем виде отношение таких отрезков биссектрисы считая от вершины угла можно представить как (a+b)/c, где в знаменателе сторона, к которой проведена биссектриса.