1.
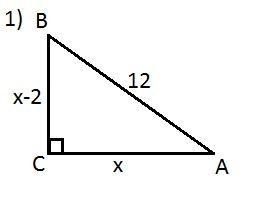
1) Пусть ΔАВС - прямоугольный, ∠С=90°, АВ - гипотенуза, АВ=12 см.
АС=х, ВС=х-2, Р(АВС)=26 см.
Составляем уравнение:
x+(x-2)+12=26;
2x-2+12=26;
2x+10=26;
2x=26-10;
2x=16;
x=8.
AC=8 см, ВС=8-2=6 (см).
Вообще, такого прямоугольного треугольника с катетами 6 см, 8 см, и гипотенузой 12 см не существует, так как не выполняется условие т.Пифагора:
6²+8²≠12²:
36+64≠144;
100≠144.
2.
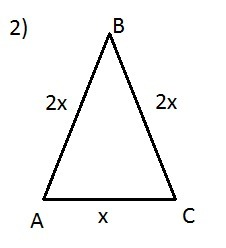
1) Пусть ΔАВС - равнобедренный, АВ=ВС=2х, АС=х, Р(АВС)=15 см.
Составляем уравнение:
2х+2х+х=15;
5х=15;
х=3.
АС=3 см, АВ=ВС=2*3=6 см.
Ответ: 6 см, 6 см.