ДАНО
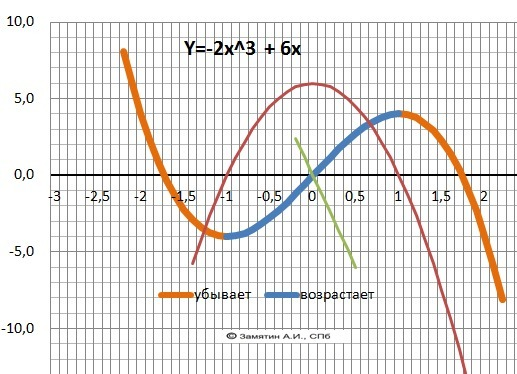
Y = -2x³ + 6x
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) или X∈R - непрерывная.
2. На четность
Y(-x) = -Y(x) - функция нечётная.
3. Пересечение с осью Х.
Y(x) 2x*(3 - x²) = 0
x1 = - √3 и х2 = 0 и х3 = √3
4. Положительна при X∈(-∞;-√3]∪[0;√3]
Отрицательна при X∈[-√3;0]∪[√3;+∞)
6. Исследование на монотонность по первой производной.
Y'(x) = -6x² - 6 = -6*(x² - 1)
Корни - х1 = -1 и х2 = 1.
Убывает - Х∈(-∞;-1]∪[1;+∞)
Возрастает - X∈[-1;1]
7. Локальные экстремумы
Минимум - Y(-1) = -4
Максимум - Y(1) = 4
8. Точка перегиба в корне второй производной
Y"(x) = -12x = 0 - график зеленого цвета.
x = 0 - точка перегиба
Вогнутая - "ложка" - X∈(-∞;0]
Выпуклая - "горка" - X∈[0;+∞)
9. Периода нет. Значения однозначны.