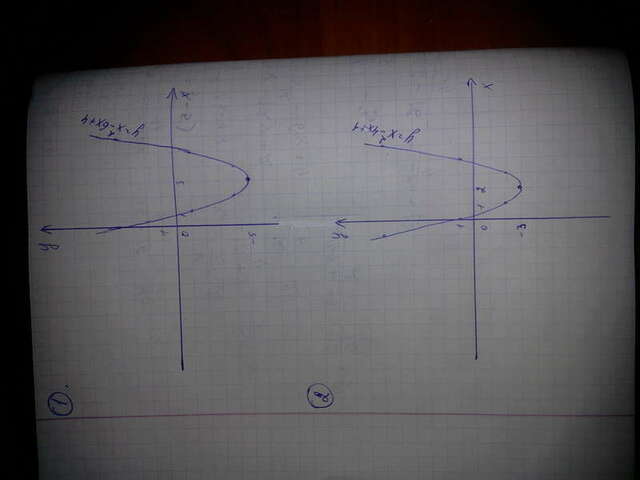
1) y=x^2-6x+4 Это парабола, ветви которой направлены вверх. Для того, чтобы её построить нам нужна вершина параболы О'(x;y)
x= -b\2a
y= -b^2+4ac\4a
для данного уравнения: a=1, b=-6, c=4
Подставляем эти значения в формулы и считаем: х=-(-6)\2*1 ; х= 6\2 =3
у=-(-6)*2+4*1*4\4*1 ; у= -36+16\4 ; у= -20\4 ; у= -5
Таким образом мы получили вершину параболы О'(3;-5) Теперь осталось лишь построить график с началом в вершине параболы.
2)Это тоже парабола, ветви вверх. Напишу вершину х=-(-4)\2*1=4\2=2
у=-(-4)^2+4*1*1\4*1= -16+4\4= -12\4= -3
O' (2;-3)
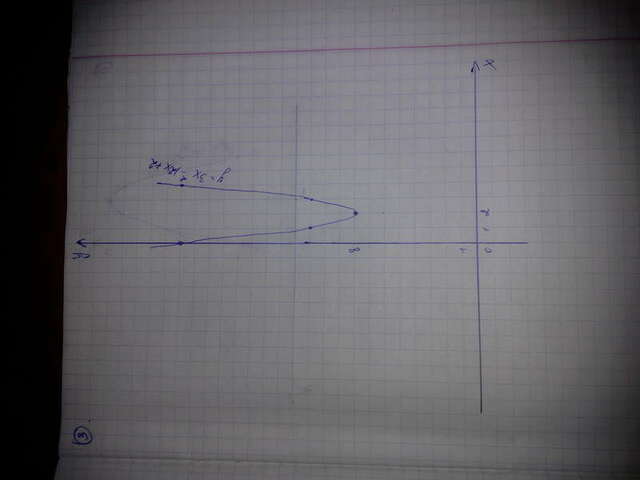
3) Это парабола ветви вверх, но она уже будет сжала в 3 раза вдоль оси ОУ (если вершина находится в начале координат (в точке (0;0)), то параболу мы обычно строим по точкам (1;1), (2;4), (3;9) и т.д. в этом же случае, мы будем увеличивать у в 3 раза, например: будет не (1;1), а (1;3), не (2;4), а (2;12) и т.д., т.е. наша парабола как бы вытянется вверх)
Вершина для неё: х=-(-12)\2*3=12\6=2
у=-(-12)^2+4*3*2\4*3= -144+48\12= 98\12 = 8
O'(2;8)
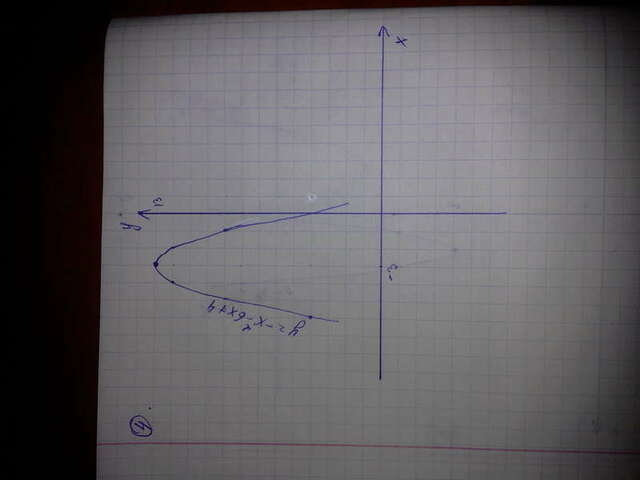
4) Это парабола, но ветви её будут направлены вниз, т.к. перед х^2 стоит "-".
Вершина: х=-(-6)\2*(-1) = 6\(-2) = -3
у= -(-6)^2+ 4*(-1)*4\ 4*(-1)= -36-16\(-4)= -52\(-4)=13
O'(-3;13)