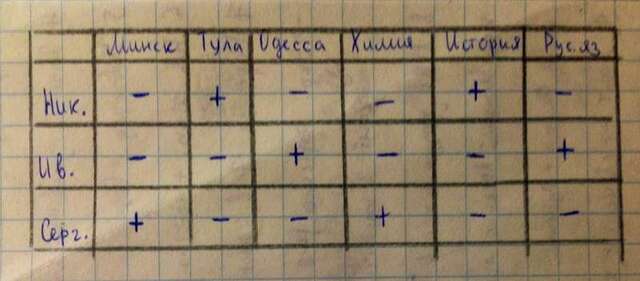
Такие задания удобно решать с помощью таблицы (приложение). Ход рассуждений:
1. Заполним таблицу по данным 1 и 4 утверждений.
2. Допустим, что Иванова живёт в Минске. Тогда она преподаёт не русский (утверждение 2). Но она не преподаёт и химию (утверждение 4). Таким образом, Иванова преподаёт историю. Но её преподаёт учитель, работающий в Туле (утверждение 3). Противоречие. Значит, Иванова живёт не в Минске. Ставим соответствующий знак в таблице.
3. Раз ни Николаева (утверждение 1), ни Иванова (п.2) не работают в Минске, значит, там преподаёт Сергеева. Поэтому она преподаёт не русский язык (утверждение 3). Ставим соответствующие знаки в таблице.
4. Раз Иванова не преподаёт ни в Минске (п.2), ни в Туле (утверждение 1), то она работает в Одессе. Ставим соответствующий знак в таблице.
5. Раз Николаева не преподаёт ни в Минске (утверждение 1), ни в Одессе (п.4), то она работает в Туле. Поэтому она преподаёт историю. Ставим соответствующие знаки в таблице.
6. Заполнить оставшиеся поля таблицы не составляет труда. Иванова преподаёт русский (так как она не преподаёт ни химию (утверждение 4), ни историю (п.5)), Сергеева - оставшуюся химию.
Ответ: Николаева - Тула, история; Иванова - Одесса, русский язык; Сергеева - Минск, химия.