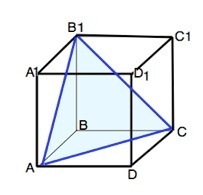
Все грани куба равны, следовательно, и диагонали граней равны. Плоскость, которая проходит через диагонали граней куба, "высекает" в нем равносторонний треугольник со стороной, равной 3√2 ( из формулы диагонали квадрата).
Площадь сечения равна площади правильного треугольника.
S=(a²√3):4
S==(3√2)²•√3:4=4,5√3 см²