Вспоминаем то, что дробь будет больше нуля, если числитель и знаменатель больше нуля или они оба меньше нуля(числитель может быть равен нулю, а знаменатель нет, ибо на 0 делить нельзя. смотрим на наше неравенство и видим то, что числитель меньше нуля и не зависит от икса. значит знаменатель должен быть тоже меньше нуля переходим к неравенству-следствию:
(x + 3)^2 - 10 < 0
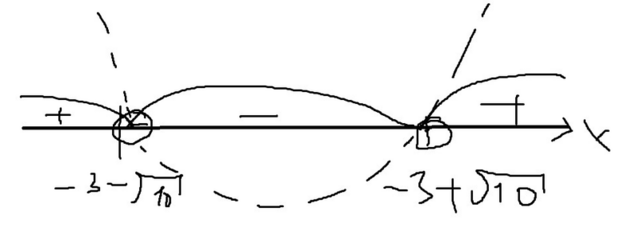
далее решаем это простое неравенство методом интервалов, но сначала найдём корни:
x^2 + 6x + 9 - 10 < 0
x^2 + 6x - 1 < 0
d = 36 + 4 = 40
x1 = (-6 + √40)/2 = -3 + √10
x2 = (-6 + √40)/2 = -3 - √10
не очень приятные корни, но что поделать
методом интервалов получаем, что x∈(-3 - √10; -3 + √10)