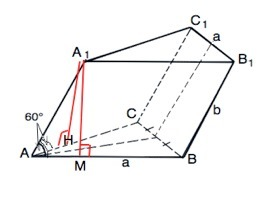
Площадь боковой поверхности призмы - сумма площадей её боковых граней.
Ребра призмы параллельны, основания призмы – параллельны, ⇒ боковые грани - параллелограммы.
Так как призма наклонная и острый угол двух соседних граней (параллелограммов) равен 60°, эти грани равны, их высоты
А1Н и А1М равны АА1•sin60°=b√3/2
Площадь каждой из этих граней S=a•h=a•b•√3/2, а их сумма a•b√3
Высота третьей грани равна боковому ребру, ⇒ третья грань – прямоугольник ВВ1С1С со сторонами а и b . Его площадь S=ab.
Площадь боковой поверхности
S=a•b•√3 +ab= ab•(√3+1)