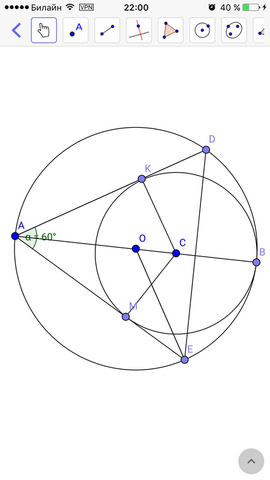
Прямоугольные треугольники АКС и АМС равны т.к. АК=АМ (как касательные из одной точки) и АС - общая сторона, значит ∠КАС=МАС.
Прямоугольные тр-ки АДВ и АЕВ равны т.к. ∠ДАВ=∠ЕАВ и сторона АВ общая, значит АД=АЕ.
В равнобедренном треугольнике АДЕ угол при вершине равен 60°, значит он правильный, вписанный в окружность с центром в точке О и радиусом R.
Для правильного тр-ка R=a/√3 ⇒ a=R√3.
Хорды АД и АЕ равны а.
Ответ: R√3.