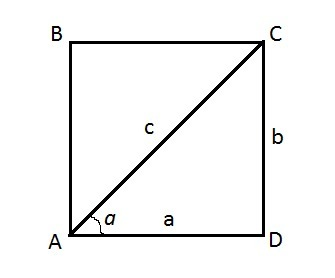
Этот тип задач подразумевает нахождение точек максимума площади в зависимости от сторон прямоугольника.
1) Площадь прямоугольника находим по формуле S=a*b.
2) Выражаем одну сторону через другую. Пусть а - длина прямоугольника, b - ширина прямоугольника, tgα=b/a, b=a*tgα⇒
S=a*a*tgα=a²tgα.
С другой стороны cosα=a/c, a=c*cosα, где с - значение гипотенузы, т.е. определенное число.
Таким образом, S=a²tgα=c²*cos²α*tgα=c²*sinα*cosα.
3) Находим первую производную и приравниваем её к нулю:
S'=(c²sinα*cosα)'=c²((sinα)'*cosα+sinα*(cosα)')=c²(cos²α-sin²α)=c²cos2α.
c²cos2α=0;
cos2α=0;
2α=π/2+πn, n∈Z;
α=π/4+πn/2, n∈Z.
Получили, что угол α=45°, а это значит, что прямоугольник имеет наибольшую площадь с определенной гипотенузой, если прямоугольник является квадратом.
а) сторона квадрата с гипотенузой 11 см равна 11=а√2, а=11√2/2.
Площадь равна S=(11√2/2)²=121*2/4=121/2 (см²).
б) сторона квадрата с гипотенузой 3 дм равна 3=а√2, а=3√2/2.
Площадь равна S=(3√2/2)²=9*2/4=9/2 (дм²).
Ответ: а) 121/2 см²; 9/2 дм².