Найти наибольшее и наименьшее значение функции: f(x)=(x^2-8x)/(x+1)на промежутке [-5;-2]

f(x)=(x^2-8x)/(x+1)
$f'(x)= \frac{(x^2-8x)'(x+1)-(x+1)'(x^2-8x)}{(x+1)^2}$
$f'(x)= \frac{(2x-8)(x+1)-(x^2-8x)}{(x+1)^2}$
$f'(x)= \frac{2x^2-6x-8-x^2+8x}{(x+1)^2}$
$f'(x)= \frac{x^2+2x-8}{(x+1)^2}$
$f'(x)= \frac{(x+4)(x-2)}{(x+1)^2}$
Найдем при каком значении икс производная равна 0
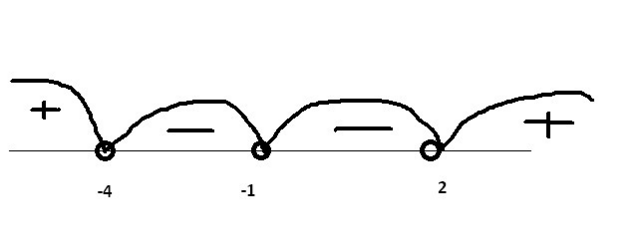
1. x = -4
2. x = 2
3. x ≠ 1

Точка максимума: -4, точка минимума: 2(не понадобится, т.к промежуток [-5;-2]

Подставляем значения

$f(-2)= \frac{(-2)^2-8*(-2)}{-1}= \frac{4+16}{-1} = -20$
$f(-4)= \frac{(-4)^2-8*(-4)}{-3}= \frac{16+32}{-3} = -16$
$f(-5)= \frac{(-5)^2-8*(-5)}{-4}= \frac{25+40}{-4} = -16,25$

Ответ: Минимальное значение: -20 при x = -2, максимальное значение: -16 при x = -4

Найти наибольшее и наименьшее значение функции: f(x)=(x^2-8x)/(x+1)** промежутке [-5;-2]