Это задание на геометрический смысл производной.
Производная в точке равна угловому коэффициенту касательной.
f`(x₀)=k
k=tgα
α- угол, который образует касательная к графику функции в точке с абсциссой х₀ с положительным направлением оси Ох.
1.
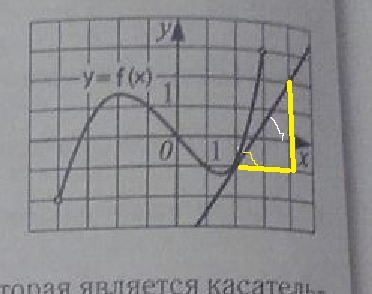
f`(x₀)=tgα=3/2
α- угол, отмеченный на рисунке дугой белого цвета.
Но удобнее найти тангенс равного ему угла, отмеченного дугой желтого цвета из прямоугольного треугольника с катетами 3 и 2
2.
f`(x)=2x-2
k=3
f`(x₀)=2x₀-2
2x₀-2=3
x₀=2,5
3.
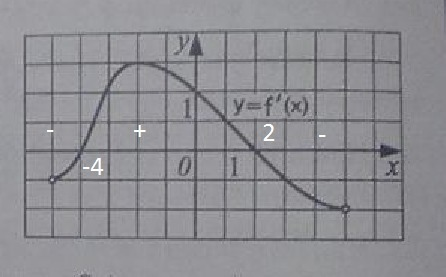
Точки, в которых производная равна нулю, являются точками возможных экстремумов.
На рисунке это точки с абсциссами -4 и 2.
Для того чтобы установить является ли точка точкой экстремума применяем достаточное условие экстремума:
если при переходе через точку производная меняет знак с - на +, то это точка минимума, если с + на -, точка максимума.
х=2- точка максимума