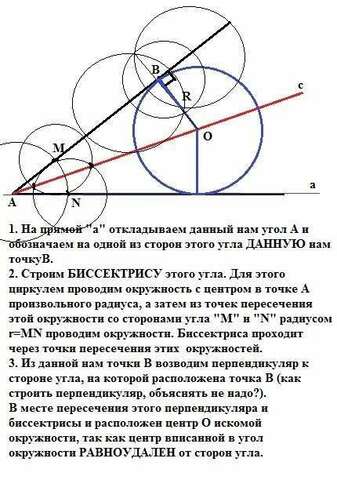
Если условие такое: "Постройте окружность которая касается сторон данного угла причем одно из касаний должно быть в данной точке на стороне угла", то решение - на рисунке..
1. На прямой "а" откладываем данный нам угол А и обозначаем на одной из сторон этого угла ДАННУЮ нам точкуВ.
2. Строим БИССЕКТРИСУ этого угла. Для этого циркулем проводим окружность с центром в точке А произвольного радиуса, а затем из точек пересечения этой окружности со сторонами угла "M" и "N" радиусом r=MN проводим окружности. Биссектриса проходит через точки пересечения этих окружностей.
3. Из данной нам точки В возводим перпендикуляр к стороне угла, на которой расположена точка В (как строить перпендикуляр, объяснять не надо?).
В месте пересечения этого перпендикуляра и биссектрисы и расположен центр О искомой окружности радиуса R=ОВ, так как центр вписанной в угол окружности РАВНОУДАЛЕН от сторон угла - то есть лежит на биссектрисе угла.