Прямоугольный треугольник с катетами 5 и 12 вращается вокруг гипотенузы. Найти объем тела...

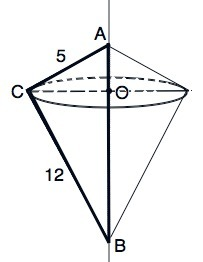
Объём получившейся при вращении фигуры равен сумме объёмов двух конусов с общим основанием, радиус которого равен высоте, проведенной из прямого угла исходного треугольника.

Гипотенуза АВ=√(AC²+BC²)=√(12²+5²)=13

Из площади прямоугольного треугольника высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Высота СО=СА•CB:AB

r=СО=60/13

V=V1+V2

V1=S(осно)•AO:3

V2=S(осн)•BO:3

V=S(AO+BO):3

AO+BO=AB=13

V=13S:3

Площадь общего основания

$S= \pi r^{2}= \frac{3600 \pi }{13*13} \\ \\ V= \frac{3600* \pi *13}{13*13*3} = \frac{1200 \pi }{13}$

Или 1200•3,14:13 ≈289,846 (ед. площади)

------

Примечание: если запись некорректно отображается, обновите страницу.